情欲禁地高清在线观看

初中毕业生学业考试数学卷巨臀 twitter

及谜底

一、填空题（每小题3分，共30分）

　　1、计较：（a－b）－（a+b）= 　　　　　 。

　　2、计较：（a2b）2÷a4 =　　　　　   。

　　3、函数中，自变量的取值界限是　　　　　　　  。

　　4、北京与巴黎两地的时差是－7小时（带正号的数暗意并吞时期比北京早的时期数），要是现时北京时期是7∶00，那么巴黎的时期是　　　　　   。

　　5、求值：sin230°+cos230°= 　　　　　  。

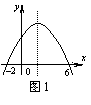
6、字据图1中的抛物线，当x　　　　  时，y随x的增大而增大，

当x　　　　  时，y随x的增大而减小，当x　　　　  时，y有最大值。

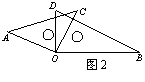7、如图2，将一副直角三角板叠在一谈，使直角过火重合于点O，则

∠AOB+∠DOC=　　　　　  。

8、已知一个三角形的三边长别离是6㎝，8㎝，10㎝，则这个

三角形的外接圆面积等于　　　　 ㎝2。

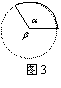
9、如图3，扇子的圆心角为α，余下扇形的圆心角为β，为了使扇子

的外形好意思不雅，不竭情况下α与β的比按黄金比例盘算，若取黄金比为0.6，

则α=　　　　度。

　 10、如图4是我市城乡住户储蓄入款余额的统计图，

　　　　 城乡住户储蓄入款余额(亿元)

300

　

　

　

　239.6

200

　

　

155.14

　

150

　

　

　

　

100

　

19.46

　

　

50

0.46

　

　

　

0

1978年

1990年

2000年

2003年

请你字据该图写出两条正确的信息：

①　　　　　　　　　　　　　　　　　　　　   ；

②　　　　　　　　　　　　　　　　　　　　   。

成人游戏

　 二、领受题（每小题3分，共15分）　　

　 11、已知⊙O的半径为5㎝，⊙O1的半径为3㎝，　　　　　　　  图4

两圆的圆心距为7㎝，则它们的位置干系是………………………………………（　　）

A、相交　　 B、外切　　 C、相离　　 D、内切

12、方程x2－5x－1=0 …………………………………………………………（　　）

A、有两个绝顶实根　　　　　　　　　 B、有两个不等实根

C、莫得实根　　　　　　　　　　　　 D、无法详情

13、一组对边平行，况兼对角线相互垂绝顶的四边形是……………………（　　）

　  A、菱形或矩形　　　　　　　　　　　 B、正方形或等腰梯形

C、矩形或等腰梯形　　　　　　　　　 D、菱形或直角梯形

14、设a是实数，则a－a的值………………………………………………（　　 ）

　  A、不错是负数　　　　　　　　　　　 B、不成能是负数

C、必是正数　　　　　　　　　　　　 D、不错是正数也不错是负数

15、由梅州到广州的某一次列车，驱动途中泊岸的车站次序是：梅州——兴宁——华城——河源——惠州——东莞——广州，那么要为此次列车制作的火车票有……（　 ）

　A、6种　　 B、12种　　 C、21种　　 D、42种

三、解答下列各题（每小题6分，共24分）

16、计较：

17、在“创优”举止中，我市某校开展集聚废电板的举止，该校初二（1）班为了揣度四月份集聚电板的个数，随即抽取了该月某7天集聚废旧电板的个数，数据如下：（单元：个）：48，51，53，47，49，50，52。求这七天该班集聚废旧电板个数的平均数，并揣度四月份（30天计）该班集聚废旧电板的个数。

18、解方程：

19、如图5，RtΔABC中，∠ACB=90°，∠CAB=30°，用圆规和直尺作图，用两种圭表把它分红两个三角形，且要求其中一个三角形的等腰三角形。（保留作图陈迹，不要求写稿法和确认）

四、（20、21两题各7分，22、23两题各8分，24小题10分，25小题11分）

20、如图6，四边形ABCD是矩形，O是它的中心，E、F是对角线AC上的点。

（1）要是　　　　　　　　  ，则ΔDEC≌ΔBFA（请你填上能使论断诱骗的一个条目）；

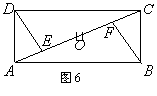（2）确认你的论断。

　  21、为精打细算用电，某学校于本学期初制定了详备的用电洽商。要是实质每天比洽商多用2度电，那么本学期的用电量将会逾越2530度；要是实质每天比洽商精打细算2度电，那么本学期用电量将会不逾越2200度电。若本学期的在校时期按110天计较，那么学校每天用电量应欺压在什么界限内？

　　22、如图7，RtΔABC中，∠ACB=90°，AC=4，BA=5，点P是AC上的动点（P不与A、C重合）设PC=x，点P到AB的距离为y。

　 （1）求y与x的函数干系式；

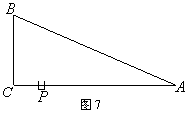　 （2）试商讨以P为圆心，半径为x的圆与AB场地直线的位置干系，并指出相应的x的取值界限。

23、东海体育用品市场为了倾销某一通纳降，先作念了市场走访，得到数据如下表：

卖出价钱x（元/件）

50

51

52

53

……

销售量p（件）

500

490

480

470

……

 （1）以x动作点的横坐标，p动作纵坐标，把表中的

数据，在图8中的直角坐标系中描出相应的点，不雅察集聚

各点所得的图形，判断p与x的函数干系式；

　 （2）要是这种通纳降的买入件为每件40元，试求销售

利润y（元）与卖出价钱x（元/件）的函数干系式

（销售利润=销售收入－买入支拨）；

　 （3）在（2）的条目下，当卖出价为若干时，能取得最大利润？

　　24、如图9，已知C、D是双弧线在第一象限分支上的两点，直线CD别离交x轴、y轴于A、B两点。设C（x1，y1）、D（x2，y2），集聚OC、OD（O是坐标有点），若∠BOC=∠AOD=α，且tanα=，OC=。

　 （1）求C、D的坐标和m的值；

　 （2）双弧线上是否存在小数P，使得ΔPOC和ΔPOD的

面积绝顶？若存在，给出确认，若不存在，确认事理。

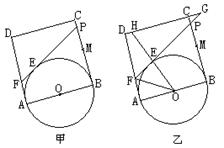
25、已知，如图10(甲)，正方形ABCD的边长为2，点M是BC的中点，P是线段MC上的一个动点， P不通顺到M和C，以AB为直径作念⊙O，过点P作⊙O的切线交AD于点F，切点为E.

（1）求四边形CDFP的周长；

（2）试探索P在线段MC上通顺时，求AF·BP的值；

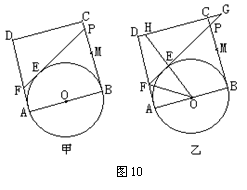（3）蔓延DC、FP相交于点G，集聚OE并蔓延交直线DC于H(如图乙)，是否存在点P，

使△EFO∽△EHG?要是存在，试求此时的BP的长;要是不存在，请确认事理。

试卷谜底

一、填空题：

　 1、－2b； 2、　　　 b2； 3、x≤2； 4、0：00；5、1； 6、x＜2，x＞2，x=2；7、180；

　 8、25π；9、135°；10、①从1978年起，城乡住户储蓄入款约束增长，②2000年到2003年城乡住户储蓄入款的增长速率较快。（谜底不惟独）

二、领受题：

  11、A； 12、B； 13、B； 14、B； 15、C

三、解答下列各题

  16、解：原式=；

17、这7天集聚电板的平均数为：（个）

　　50×30=1500（个）

　　∴这七天集聚的废旧电板平均数为50个，四月份该班集聚的废电板约1500个。

18、解：解法一：原方程可化为：， ∴ x (2x+1)=2 (X+1)2 解得：

　　　　　　  经考核可知，的原方程的解。

　　　 解法二：设，则原方程化为：y2+y－2=0 ， ∴ (y+2)(y－1)=0

　　　　　　　 ∴y=－2或y=1

　　　　　　　 当y=－2时，，解得:

　　　　　　　 当y=1时， ，方程无解

　　　　　　　 经考核可知，的原方程的解。

19、解：作法一：作AB边上的中线；

　　　　作法二：作∠CBA的瓜分线；

　　　　作法三：在CA上取小数D，使CD=CB。

　　　　　　　 

20、解：（1）AE=CF（OE=OF；DE⊥AC；BF⊥AC；DE∥BF等等）

　　　 （2）∵四边形ABCD是矩形，∴AB=CD，AB∥CD，∠DCE=∠BAF

　　　　　 又∵AE=CF，∴AC－AE=AC－CF，∴AF=CE，∴ΔDEC≌ΔBAF

21、解：设学校每天用电量为x度，依题意可得：

　　　　解得：，即学校每天用电量应欺压在21度～22度界限内。

22、解：（1）过P作PQ⊥AB于Q，则PQ=y

　　　　　 ∵∠A=∠A，∠ACB=∠AQP=90°

　　　　　 ∴RtΔAQP≌ΔRtΔACB， ∴PQ∶BC=AP∶AB

　　　　　　 依题意可得：BC=3，AP=4－x

∴ 　化简得：

　　　　  （2）令x≤y，得：，解得：

∴当时，圆P与AB场地直线相离；

　  时，圆P与AB场地直线相切；

　  时，圆P与AB场地直线相交。

　 23、解：（1）p与x成一次函数干系。 设函数干系式为p=kx+b ，则

　　　　　　  解得：k=－10，b=1000 ， ∴ p=－10x+1000

经考核可知：当x=52，p=480，当x=53，p=470时也适宜这一干系式

∴所求的函数干系为p=－10x+1000

　　　　　 （2）依题意得：y=px－40p=(－10x+1000)x－40(－10x+1000)

∴ y=－10x2+1400x－40000

(3)由y=－10x2+1400x－40000 可知，当时，y有最大值

　 ∴ 卖出价钱为70元时，能花得最大利润。

　 24、解：（1）过点C作CG⊥x轴于G，则CG=y1，OG=x1 ，

在RtΔOCG中，∠GCO=∠BOC=α，∵，

∴ 即又∵

∴ ，即，

解得：x1=1或x1=－1（分歧舍去）

∴x1=1，y1=3，∴点C的坐标为C（1，3）。

又点C在双弧线上，可得：m=3

过D作DH⊥y轴于H，则DH=y2，OH=x2

在RtΔODH中， ，

∴ 即　又∵ x2y2=3  解得：y2=1或y2=－1（分歧舍去）

∴x2=3，y2=1，∴点D的坐标为D（3，1）

　　　　  （2）双弧线上存在点P，使得，

这个点便是∠COD的瓜分线与双弧线的交点

∵点D（3，1），∴OD=，∴OD=OC

　点P在∠COD的瓜分线上，则∠COP=∠POD，又OP=OP

∴ΔPOC≌ΔPOD ，∴

25、解（1）∵四边形ABCD是正方形∴∠A=∠B=90°，

∴AF、BP齐是⊙O的切线，

又∵PF是⊙O的切线

∴FE=FA，PE=PB

∴四边形CDFP的周长为：

AD+DC+CB=2×3=6

(2 ) 集聚OE，PF是⊙O的切线

∴OE⊥PF.在 Rt△AOF和Rt△EOF中，

∵AO=EO，OF=OF

∴Rt△AOF≌Rt△EOF ∴∠AOF=∠EOF，

同理∠BOP=∠EOP，∴∠EOF+∠EOP=180°=90°，∠FOP=90°

即OF⊥OP，∴AF·BP=EF·PE=OE2=1

(3 )存在。∵∠EOF=∠AOF，∴∠EHG=∠AOE=2∠EOF，

∴当∠EFO=∠EHG=2∠EOF， 即∠EOF=30°时，Rt△EFO∽Rt△EHG

此时，∠EOF=30°， ∠BOP=∠EOP=90°-30°=60°∴BP=OB·